1403. Baloo arithmetic
Balu, a lazy brown bear who teaches wolves the
Law of the Jungle. He can wander where he pleases, because he eats only nuts, honey and roots.
This happened at
the time when Baloo the bear taught Mowgli the Law of the Jungle. A large and
important brown bear rejoiced at the abilities of a student, because wolf cubs
usually learn from the Law of the Jungle only what their Pack and tribe need.
But Mowgli, like a baby cub, needed to know much more.
In class on
arithmetic, Baloo came up with the next game. It was necessary to get the
number n from the number 1,
while allowing the current number to be either multiplied by 3,
or 4 to be added to the current number. For each multiplication,
Baloo gave 5 cuffs, and for each addition 2 cuffs. For example,
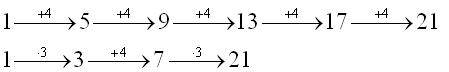
in the first case
one gets 10 cuffs, in the second case one gets 12 cuffs.
Mowgli naturally
mastered arithmetic the best of all and quickly figured out how to solve a
problem, having received the least number of cuffs. He also noticed that it is
not always possible to complete the task of a cunning bear ...
Input. One integer n (1 ≤ n
≤ 109).
Output. Print the
minimum number of cuffs that can be obtained for solving the problem. If the
problem cannot be solved, then output number 0.
|
Sample
input |
Sample
output |
|
21 |
10 |
SOLUTION
data structures – map,
recursion
Algorithm analysis
Let f(n) be the minimum number of cuffs that can be
obtained for solving the problem.
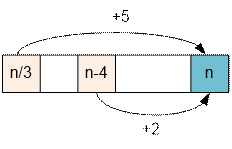
Then:
·
f(n) = min (f(n / 3) + 5, f(n – 4) + 2 ), if n is divisible by 3.
·
f(n) = f(n – 4) + 2 , if n is not divisible by 3.
For example, for n ≤ 107 compute and store the values of the function f(n) in the linear array m. For large values of n, do the memoization in the structure map.
Algorithm realization
Declare the structures
for storing the values of the function f(n).
#define MAX 10000000
int m[MAX];
map<int,
int> mp;
Function f is
implemented recursively with memoization.
int f(int n)
{
if (n < MAX) return
m[n];
if (mp[n] > 0) return
mp[n];
if (n % 3 == 0)
mp[n] = f(n/3) + 5;
else
mp[n] = f(n-4) + 2;
return mp[n];
}
The main part of the program. Let m[i] = - µ, if Mowgli
cannot get the value i by any actions. Compute the values of f(i) for i up to 107 and store them in m[i].
m[0] = -MAX; m[1] = 0; m[2] = -MAX; m[3]
= 5; m[4] = -MAX; m[5] = 2;
for(i = 6; i < MAX; i++)
if(i % 3 == 0)
m[i] = min(m[i / 3] + 5, m[i - 4] + 2);
else
m[i] = m[i - 4] + 2;
Read the input value of n. Compute and print the answer.
scanf("%d",&n);
res = f(n);
If res is less than 0, then it is
impossible to solve the problem, print the number 0.
if (res < 0) res = 0;
printf("%d\n",res);
Java realization
import java.util.*;
public class Main
{
static Map<Integer, Integer> mp = new HashMap<Integer, Integer>();
static int MAX = 10000000;
static int m[] = new int[MAX];
public static int f(int n)
{
if (n < MAX) return m[n];
if (mp.containsKey(n)) return mp.get(n);
if (n % 3 == 0)
mp.put(n,f(n/3) + 5);
else
mp.put(n,f(n-4) + 2);
return mp.get(n);
}
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
m[0] = -MAX; m[1] = 0; m[2] = -MAX; m[3] = 5;
m[4] = -MAX; m[5] = 2;
for(int i = 6; i < MAX; i++)
if(i % 3 == 0)
m[i] = Math.min(m[i / 3] + 5, m[i - 4] + 2);
else
m[i] = m[i - 4] + 2;
int n = con.nextInt();
int res = f(n);
if (res < 0) res = 0;
System.out.println(res);
con.close();
}
}